ESTADÍSTICA
Por cortesía de @jrlr
Índice de contenidos
Pregunta 174
En un contraste de hipótesis estadístico, ¿a qué definición -corresponde con mas exactitud el valor “p”?
- La probabilidad de observar los resultados del estudio, u otros más alejados de la hipótesis nula, si la hipótesis nula fuera cierta.
- La probabilidad de que la hipótesis nula sea cierta.
- La probabilidad de observar los resultados del estudio si la hipótesis nula fuera cierta.
- La probabilidad de que los resultados observados sean debidos al azar.
- La probabilidad de observar los resultados del estudio, u otros más alejados de la hipótesis nula, si la hipótesis alternativa fuera cierta.
Comentario:
La respuesta más correcta es la 1. La justificación de la respuesta es simple; por definición, el valor de p es lo que se indica en esa respuesta. Se puede comprobar por ejemplo en el siguiente enlace. También es la que se recoge en numerosos libros.
Técnicamente, se debe recordar que lo que se somete a evaluación en un contraste de hipótesis es la llamada hipótesis nula, lo que excluye la respuesta 5. Por otro lado, la afirmación de la respuesta 2 no es viable; nunca podemos decir si una hipótesis es cierta, al menos cuando se trabaja en inferencia, pero si que podemos declararla falsa.
La respuesta 3 es muy parecida a la 1, pero solamente contempla que un resultado sea igual al propuesto por la hipótesis nula, pero no aquellos que sean más extremos que el propuesto.
La respuesta 4 se encuentra en (malos) libros de texto sobre estadística, aunque no recoge los matices de que esos resultados se observan bajo la premisa de que la hipótesis nula es cierta.
Pregunta 175
En una población, el valor medio del colesterol total es de 216 mgldL, con una desviación típica de 5 mgldL. El porcentaje de personas cuyo nivel de colesterol es mayor de 226 mgldL es, aproximadamente:
- El 0,025%.
- El 0,5%.
- El 2,5%.
- El 5%.
- El 10%.
Comentario:
Se trata de aplicar las propiedades de la distribución normal. Una de ellas es que la curva es simétrica con respecto a la media. Por otro lado, en la tabulación de los valores de una normal, se verifica que en el intervalo entre media-2 desv. típicas y media+ 2 desv. típicas se incluyen al 95% de la población.
Aplicando esas propiedades a este ejemplo, entre 216-2*5 y 216+2*5, es decir entre 206 y 226 se encuentran el 95% de los individuos. El 5% restante se reparte por debajo de 206 y por encima de 226, a partes iguales. Es decir, que por encima de 226 queda un 5%/2 = 2,5%.
La respuesta correcta es la 3.
Pregunta 176
La prueba kappa o test de Cohen:
- Mide la validez interna de una prueba diagnóstica.
- Mide la validez externa de una prueba diagnóstica.
- Se mantiene estable para una misma prueba diagnóstica al modificar la frecuencia de la enfermedad.
- Se mantiene estable para una misma prueba diagnóstica tanto si se utiliza como cribado o prueba clínica.
- Tiende a disminuir su valor al aumentar el número de categorías de la prueba diagnóstica.
Comentario:
El coeficiente kappa es una medida de concordancia entre observadores. Por ese motivo, para mi la respuesta correcta es la 5, ya que se refiere a una característica de esta medida. Quien quiera que se lo confirme le ofrezco un documento donde lo puede comprobar si mira en la página 6.
El resto de respuestas se refieren a la validez de las pruebas diagnósticas, que se valoran mediante la sensibilidad y la especificidad.
Pregunta 177
¿Cuál de los siguientes parámetros mide el apuntamiento de una distribución?
- El coeficiente de Fisher.
- Los cuartiles.
- La varianza.
- La curtosis.
- La amplitud.
Comentario:
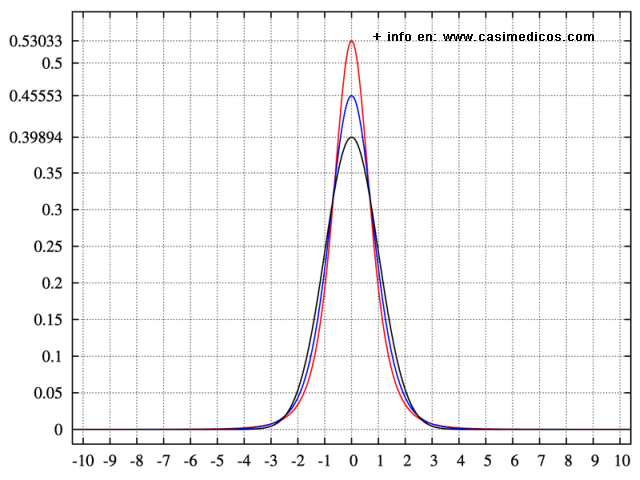
Por definición, la curtosis se define como una medida del grado de apuntamiento de una distribución. Por lo tanto, la respuesta correcta es la 4. Se puede comprobar en el siguiente enlace.
En la gráfica aparecen tres curvas, con distintos grados de curtosis: platicúrtica (negro), mesocúrtica (azul) y leptocúrtica (rojo).
El término apuntamiento es más bien descriptivo. De una forma más técnica, la curtosis mide la concentración de las observaciones alrededor de la media, relacionándola con la varianza de las observaciones.
Las restantes respuestas se excluyen porque tanto la varianza como la amplitud son medidas de dispersión o variabilidad de las observaciones, y los cuartiles son medidas de posición.
El coeficiente de Fisher supongo que se refiere al coeficiente de simetría. Aunque también es una medida de forma, como la curtosis, se refieren a otro aspecto. El coeficiente de simetría mide cómo se reparten las observaciones con respecto a la media, pero examinando si las observaciones están igualmente repartidas por encima y por debajo de la media (curva simétrica) o no lo están (curva asimétrica).
Pregunta 194
Una de las siguientes afirmaciones sobre el meta-análisis de ensayos clínicos es cierta:
- La posible heterogeneidad de los estudios incluidos se suele examinar con el método conocido como el gráfico en embudo (funnel plot).
- Una de las desventajas de los modelos de efectos aleatorios es que conceden un peso excesivo a los estudios con pequeño tamaño muestral.
- El meta-análisis consiste en el análisis estadístico del conjunto de resultados obtenidos en un ensayo clínico sobre diferentes cuestiones.
- El análisis de sensibilidad no sirve para evaluar el sesgo de publicación.
- No es necesario valorar la calidad de los estudios incluidos.
Comentario:
La selección de la respuesta correcta me obliga a justificar la exclusión de las restantes. La primera respuesta es incorrecta porque el diagrama de embudo es un procedimiento para detectar el sesgo de publicación. La heterogeneidad se puede estudiar gráficamente pero con el forrest plot.
La respuesta 3 contradice al concepto de meta-análisis. No se trata de agregar los resultados de un único ensayo clínico, aunque se refieran a distintos aspectos, sino a la agregación de los resultados de varios (más de uno) ensayos clínicos, eligiendo aquellos resultados comunes recogidos en esos estudios.
La respuesta 4 la marco como incorrecta, aunque alguien podría decir lo contrario. Veamos, el análisis de sensibilidad pone a prueba los datos analizados con los ensayos disponibles. El análisis de sensibilidad es un procedimiento que nos puede ayudar a valorar cómo se modificarían nuestros resultados si faltasen estudios. Un ejemplo de este tipo de análisis es el que aparece en este estudio.
Sin embargo, si uno se pone a afinar, no se puede someter a este tipo de análisis si no tenemos constancia de que no disponemos de estudios no publicados. Pero, como hay que decidir, digo que esta respuesta es incorrecta.
La respuesta 5 es otro monumento a la ambigüedad. El estudio de la calidad de los estudios es uno de los aspectos que le da solidez a las conclusiones de un meta-análisis, especialmente si hay heterogeneidad entre los estudios. Para mi, esta fase se debe incluir siempre, por eso marco esta respuesta como incorrecta. Ahora bien, necesario, necesario, no lo es si lo que se quiere es agregar los resultados de varios estudios.
Por exclusión quedaría la respuesta 2, pero también está justificado porque en el método de efectos aleatorios, la condición por la que se pondera es por la varianza intraestudio y la varianza entre-estudios. Por esa razón, los estudios con pequeño tamaño muestral pueden pesar exageradamente en comparación con los que tienen mayor tamaño. Por corroborar que esta interpretación puede ser correcta, he mirado el siguiente artículo, que confirmaría esta interpretación.
En el Ministerio debe existir algún individuo encantado consigo mismo, y que lo demuestra preparando preguntas como ésta. Y lo digo porque tanto por el formato negativo (elegir la respuesta correcta) como por el contenido en si. Para contestarla hay que conocer bien un método, el meta-análisis, del que hay pocas personas que publiquen en nuestro país. Y lo que es más sorprendente es que se refiere a un aspecto bastante especializado dentro de la técnica.
Pero qué le vamos a hacer. El sistema permite que algún acomplejado, con necesidad de demostrar su superioridad, pueda colar sus preguntas.
fuente