Estadística
Por cortesía de @jrlr del blog Malditas mentiras y estadísticas
La numeración corresponde a la Versión 7 del examen
Pregunta 33 (vinculada a la imagen nº 17).

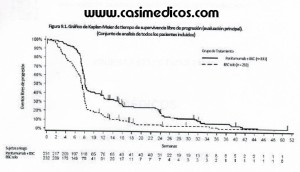
La siguiente figura describe la función de supervivencia de la variable progresión libre de enfermedad (Progression-free Survival, PFS) mediante el método de Kaplan-Meier de dos grupos de pacientes. Grupo A: pacientes tratados con el mejor tratamiento de soporte (Best Suportive Care, BSC). Grupo B: pacientes que además de BSC reciben Panitumumab. Datos complementarios a la figura: pacientes con progresión de enfermedad: Grupo A=184/232 (79%), Grupo B=161/231 (70%). Porcentaje de censuras: Grupo A=24/232 (10%), Grupo B=38/231 (16%). Prueba de log-rank p<0.0001, Hazard Ratio [95%CI]: 0.54 [0.44-0.66]. Cuál de las siguientes afirmaciones es correcta:
- La ganancia en términos de mediana de tiempo hasta la progresión en el Grupo B, no llega a superar dos semanas en relación al Grupo A.
- Para interpretar los resultados de estas dos curvas de supervivencia es necesario y suficiente la evaluación y contraste de los porcentajes de progresión, es decir 79% en el Grupo A versus 70% en el Grupo B.
- El ratio de las medianas en el tiempo hasta progresión de los dos grupos de tratamiento es 0.54.
- La prueba de log-rank evalúa la diferencia promedio en el tiempo de seguimiento.
- Los resultados de la prueba de log-rank y la estimación del Hazard Ratio (intervalo de confianza al 95%, IC95%), no son compatibles puesto que el primero indica que las diferencias son significativas mientras que el segundo no lo son.
Respuesta
La 1.
Comentario
Reconozco que esta pregunta me atrae desde el punto de vista psicométrico. El planteamiento intenta valorar la capacidad de razonamiento del que responde. La raiz de la pregunta da suficientes detalles. Todo ello la haría candidata a una buena pregunta, en comparación con el resto de preguntas de Estadística, si no fuera porque…
Uno no sabe muy bien qué es lo que se pretende preguntar. Las respuestas son tan diferentes que uno no sabe muy bien qué se persigue.
Observando el gráfico uno puede apreciar “a ojo” que la supervivencia mediana (es decir, cuando han muerto o como este caso, han recaido, es del 50%) corresponde a unas 7 semanas en el grupo A, y unas 8.5-9 semanas en el grupo B.
El resto de respuesta, a pesar de lo enrevesado de su redacción se podrían excluir porque no son totalmente correctas. La respuesta 2 es incorrecta porque solamente con las tasas no se pueden comparar las curvas de supervivencia, sino que tenemos que conocer cuándo se van produciendo los éxitus y los datos censurados (de ahí lo de análisis de supervivencia).
La 3 podría ser, pero mirando los valores medianos, no creo que la ratio sea tan baja; si tuviera ese valor, la mediana en un grupo sería el doble que la del otro grupo.
La 4 es una respuesta de concepto, que creo que se puede excluir sin mirar la gráfica. El test de log-rank no evalúa realmente el tiempo de supervivencia, sino que va comparando los riesgos de muerte en cada grupo en cada momento. Pero tal como está redactada, podría interpretarse de cualquier manera.
La 5 se elimina directamente porque no existe tal contradicción, ya que ambos límites del intervalo de confianza están por debajo de 1.
Pregunta 34 (vinculada a la imagen nº 17).
Cuál de las siguientes afirmaciones es correcta:
- Todos los pacientes del estudio excepto uno han presentado progresión de la enfermedad a las 50 semanas de seguimiento.
- Dado que al final del tiempo de seguimiento se solapan las curvas de supervivencia, no se debería describir los resultados como estadísticamente significativos.
- La reducción del riesgo de progresión de la enfermedad en el grupo B (BSC + panitumumab) es del 46% con respecto al grupo A (BSC solo).
- El promedio de tiempo hasta la progresión es el mejor estimador del efecto de los tratamientos y la diferencia entre grupos debería indicarse para evaluar su relevancia.
- El análisis de Hazard Ratio no es aceptable puesto que el porcentaje de censurar es distinto entre grupos, p<0.0001.
Respuesta
La 1.
Comentario
De nuevo la pregunta me ha decepcionado, porque recurre a una mera identificación de un elemento en el gráfico. Supongo que así lo habrán querido hacer más fácil. Pero me parece que se puede evaluar la capacidad para razonar por otros caminos.
Si se observa en la parte inferior de la gráfica, en la que se indica el número de pacientes en riesgo en cada momento, se puede observar que a partir de la semana 50 solamente queda un único paciente en riesgo, o dicho de otra forma, que el resto ha progresado.
El resto de las respuestas se pueden excluir, aunque de nuevo están redactadas de tal manera que uno no sabe muy bien qué es lo que se quiere preguntar.
Pregunta 49. En un ensayo clínico de un fármaco antineoplásico se observa un importante aumento de los niveles plasmáticos de LDL (lipoproteinas de baja densidad). Señalar de entre las siguientes afirmaciones cuál es correcta en Ia interpretación y consecuencias de este hecho:
1. Las LDL representan la forma de transporte del colesterol del intestino al hígado. Por tanto, reflejan una mayor incorporación de colesterol desde la ingesta lipídica.
2. Las LDL están implicadas en el transporte reverso del colesterol desde los tejidos periféricos hacia el hígado. Por tanto, unos niveles elevados son beneficiosos para disminuir los niveles plasmáticos de colesterol.
3. Las LDL son ricas en triglicéridos y pobres en colesterol, Un aumento de LDL en plasma refleja un aumento de síntesis de novo y/o de ingesta de triglicéridos.
4. Un aumento de los niveles de LDL en plasma es beneficioso porque protege a las arterias de la formación de placas ateroscleróticas.
5. Las LDL transportan colesterol desde el hígado a los tejidos periféricos, donde entran en las células mediante procesos de endocitosis.
Respuesta y Comentario
Pendientes … ¿Tu cual crees que es la correcta?
Pregunta 189. ¿Cuál de las siguientes aseveraciones sobre el meta-análisis es correcta?
- El objetivo del meta-análisis es resumir cuantitativamente los resultados de los estudios realizados.
- El meta-análisis es un ensayo clínico de grandes proporciones.
- Sería deseable evitar los ensayos clínicos negativos, así como los no publicados, para impedir sesgos de selección.
- Por definición, todos los meta-análisis son una fuente fidedigna de evidencia, siendo irrelevante la calidad de los ensayos o si incluyen los resultados de ensayos clínicos aleatorizados.
- El meta-análisis subsanará los errores de realización de los ensayos.
Respuesta
La 1.
Comentario
Esta pregunta tiene esa respuesta obvia. El resto de respuestas se refieren a lo que el meta-análisis NO es o lo que tiene que evitar.
Pregunta 195. El coeficiente de correlación de Pearson indica que existe asociación estadística entre dos variables cuando:
- Su valor es positivo.
- Su valor está entre -1 (menos uno) y 1(uno).
- Su valor se aproxima a cero.
- Su valor es igual o muy similar al tamaño muestral utilizado para su cálculo.
- Su valor se acerca a sus valores extremos posibles, -1 (menos uno) o 1 (uno).
Respuesta
La 5.
La respuesta 1 solamente indica el sentido de la relación, pero no si es intensa o no lo es; además, puede existir asociación inversa, y en ese caso el valor sería negativo. Es decir, que un valor positivo no indica necesariamente que hay asociación.
La respuesta 2 enuncia que los valores del coeficiente están acotados entre esos -1 y +1, pero no si hay asociación.
La respuesta 3 indica precisamente la situación contraria; cuando el coeficiente se aproxima a cero, indica que son independientes.
La respuesta 4 es errónea, porque el valor del coeficiente no está determinado por el tamaño de la muestra.
Pregunta 207. Un Pediatra desea estudiar el sobrepeso en los niños de 14 años, según los valores del IMC (índice de masa corporal). Para estimar el tamaño muestral necesario propone un nivel de confianza del 95% y una precisión de 1 unidad de IMC. ¿Qué más parámetros necesita conocer para determinar el tamaño muestral?
- La media del IMC en la población.
- La varianza del IMC.
- La media y la desviación típica del IMC.
- El tamaño de la población y la media del IMC.
- La desviación típica del IMC y el tamaño de población.
Respuesta
La 2. (dudando con la 5).
Comentario
Un ejemplo de que algunos no saben en lo que están pensando cuando ponen preguntas. Si quería medir la capacidad de razonamiento de los examinados, su capacidad para relacionar conceptos, explorar nuevas visiones de los problemas, en fin que demuestren que los futuros especialistas tienen una capacidad intelectual suficientemente acreditada, pues quien haya preparado esta pregunta desde luego no lo ha conseguido.
Hay que ser cretino para preguntar sobre una fórmula, porque lo único que se demuestra es que el que acierta se la sabe, pero poco más. La fórmula para calcular el tamaño de la muestra para variables continuas es la siguiente:
Por lo tanto, si nos dan la precisión, lo único que nos hace falta es la varianza. En esa fórmula, E = precisión (1 unidad de IMC) y Z = 1,96 porque el intervalo es del 95% (ese valor es el que corresponde a la puntuación en una curva normal).
De todas formas, la pregunta está relativamente mal redactada, porque parece que lo que quiere estudiar el Pediatra (que lo ponen en mayúsculas en el cuadernillo) es la prevalencia de malnutrición, y entonces sería una fórmula distinta.
Por otro lado, no indican si el investigador quiere hacer un estudio para una población definida, población finita, o para una población que se considere infinita. Si se trata del primer caso, entonces necesitaríamos también el tamaño de la población. Por eso he puesto que dudo con la respuesta 5, aunque me inclino por la 2, dado que no precisa nada al respecto.
fuente
http://trib.us.es/jrlacalle/